Interferometry: How light is combined from multiple telescopes
1. Introduction: Interference
The terms "interferometry'' and "interferometer'' are both derived
from the word interference. Interference is a phenomenon that occurs when one
has waves of any kind -- sound waves, light waves, ocean waves, seismic waves
from earthquakes -- it makes no difference. Whenever two waves comes together
at the same time and place, interference occurs. Resonance, beat frequencies,
hetrodyning, dissonance, are also all interference phenomena.
Interference can be visualized as the adding together of two waves with each
other. Depending on wave size (amplitude) and the degree to which they are in
or out of step with each other (phase), they will either add together or cancel.
The canceling out is still really an "addition''; in this case, it's like
adding plus one to minus one.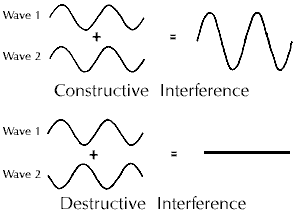 
In astronomy, we will be dealing with the interference of two light waves. If
both waves are in step or in phase, that is, the crest of both waves coincide,
the two will add together to form a single wave. This combined wave will have
a higher crest and deeper trough (or larger amplitude). In the case of light
waves, two dimmer light beams will add together to form a brighter beam -- this
is called constructive interference.On the other hand, destructive interference
occurs when the two waves are out of step with each other; that is, the crest
of one coincides with the trough of the other. Here, although the waves are
still adding together, they cancel each other out. So, the amount of interference
that occurs depends on both the amplitudes of the two waves and the degree to
which their respective crests and troughs are in phase with each other.
2. Interferometry and interferometers
Interferometry is the use of interference phenomena for measurement purposes,
either for very small angles or for tiny distance increments (the displacement
of two objects relative to one another).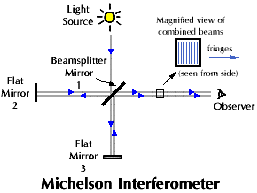 
An interferometer is a device to make such measurements. Though there are many
different types and designs of interferometers, virtually all of them operate
on the same basic principle. From a beam of light coming from a single source
(a star, a laser, a lamp, etc.), two or more flat mirrors are used to split
off (or ``pick off'') different light beams. These beams are then combined so
as to interfere with each other.
What is looked for are alternating bands of light and dark, called fringes.
Fringes are bright where the beams are constructively adding together and dark
where they are canceling each other out.
One well-known basic design for an interferometer is the Michelson interferometer,
invented by the American physicist, Albert Michelson (1853-1931), famous for
the Michelson-Morely Experiment which supports the Theory of Relativity by Einstein.
Michelson also performed experiments at Mount Wilson measuring the speed of
light. Basically, in the Michelson interferometer, one is looking "down''
along the axis of two combined beams towards the light source. A beamsplitter
mirror is used to bring the beams together from the two flat mirrors. It has
a deliberately thin reflective coating to permit about one-half of the light
to pass through. If the light is of a single wavelength, fringes will form all
along the optical axis of the combined beams, oriented perpendicular to this
axis and will appear to stand still, even though the beams are traveling at
the speed of light -- a standing wave phenomenon. To the eye, the fringes appear
as alternating small rings of light and dark surrounding the central images
of the light source.
What makes the interferometer such a precise measuring instrument is that these
fringes are only one light-wavelength apart. In visible light, about 590 nanometers
--that corresponds to 1/43,000th of an inch! Any movement along the optical
axis by either flat mirror will cause the fringes to shift an equal amount in
lockstep. The measurement of this movement is made by literally counting the
number of fringes - each dimming and brightening of light - one wavelength at
a time!
Such a precise system is also incredibly sensitive -- so much so that any vibration,
movement, thermal expansion, etc. is picked up as well. In fact, Michelson's
early experiments were affected by street traffic vibrations up to 1,000 feet
away! Using shorter wavelengths of light allow greater precision, but are much
more difficult to work with (the fringes are closer together).
3. Applying interferometry to astronomy
The application of interferometry to astronomy is very challenging. First, light
from stars isn't monochromatic -- a star's spectrum shows that light is emitted
all across the visible wavelength and beyond. Since pure fringes only exist
where all the wave crests and troughs are the same distance apart, and the fringe
spacing also varies with the light's wavelength, the combination of light from
all over the spectrum means that the interference will be smeared out into essentially
noise.
However, nature has given us a way out. There is one point where all of the
crests and troughs come together. This location is precisely on the light path
exactly in between the two pickoff mirrors. Here, there is a center fringe named
the "primary'' fringe (it's also the brightest), flanked by two secondary
fringes. These in turn are flanked by two fringes and so on, until the rest
get lost in the background nois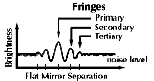e.
In astronomical interferometry, the most important parameter is the "baseline,"
the distance between the flat mirrors. Another key parameter is called "visibility,''
which is the difference in brightness between a fringe and the relative darkness
between it and the next fringe.
If one plots visibility versus baseline, the maximum visibility occurs at a
baseline of zero, and decreases as baseline is increased. At some point, the
visibility drops to zero (and the fringes disappear). This is called the "resolving
point.'' At greater baselines, the fringes reappear and visibility increases,
but only to about 10% of the peak visibility before dropping again. The heights
of subsequent peaks taper off.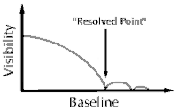 
The significance of the resolving point is that if you are observing a star,
it gives a direct measurement of the apparent diameter of the object against
the sky. If the distance to the star is known, then the actual diameter can
be calculated. (By analogy, the apparent size of coin held up varies by the
distance you hold the coin up from your eye.) Although stars are large, they
are at very great distances, and so the apparent diameters are very small, typically
a few thousandths of an arcsecond (1 milliarcsecond is about 275 billionths
of a degree).
|
